Academic-Capital

Gupta and Kabundi (2010) started with an interesting question on which macroeconomic models are most likely to predict economic growth and success. Decision-makers that have tools are better able to make current decisions that are likely to foster greater growth in the future. The researcher used emerging markets of South Africa but these same models may apply to economic hubs and the factors that predict their success.  Models are simply explanations that attempt to predict activities within the environment. Some models are more successful than others. Success is determined through a process of validity where multiple researchers over a period of time analyze the same phenomenon over and over in multiple ways to determine if the model makes sense.  Common data points in measuring economic development include per capita growth rate, consumer price index (CPI), inflation, the money market rate, and the growth rate of nominal effective exchange rates. These data points often

Projecting markets can be difficult for executives who want concrete answers to the potential decisions they are about to make. One of the strong signs of leadership is the ability to deal with ambiguous information. This means that decision makers may not have all of the information they need to make appropriate decisions. Each decision leads to the possibility of failure with significant financial costs. The use of statistical methods can be an enhancement to the decision making process through lowering levels of uncertainty. However, statistics alone can cause mistakes and are not substitutes for good judgment. Using multiple statistical analyses to make expensive projection calls can lower decision errors and lead to stronger choices that improve market choices.   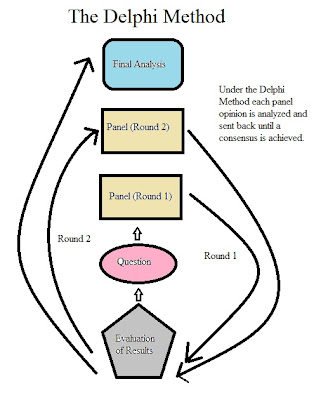The Delphi Method: The Delphi Method was developed by Olaf Helmer while at the Rand Corporation. In the method participants answer questions about predictions, products, or services while not being able to i